Rhombile Tiling

Rhombile tiling is an old tiling deisgn that you can see in a variety of places and so I decided to try coding this with a variety of options to see what I could come up with. In my daily life I see this in my gas range cover at home, and on the ceiling in Tokyo bus station - you can come across it anywhere basically. It’s probably one of the most common tiling patterns in the world. Coding this is a not-so-difficult challenge, and the interest for me has been in how to code a variety of complex shapes and designs using this very common pattern.

Checkout the repository here, and my mosaic generator here.

Some basic Trigonometry

Each rhombile block or cube forms a hexagon, and all the three pieces are the same shape but in different rotated positions. I coded a rhombile cube by forming the hexagon on top of a rectangular block. The maths and logic were as follows:

1. The total width of the rhombile “cube” would be the width of the svg container rectangle. (This width would be calculated by dividing the total mosaic area width by the number of cubes that should form a single row. In my mosaic generator I call this the density of the tiles.)
2. The rhombus used in the standard rhombile tiling pattrern has a 60 degree angle, on the sharp edge, and a 120 angle, on the wider edge.
3. So, by dividing the rhombus into triangles, the triangle would have a 30 degree angle at its acute corner. And by using basic trigonometry, the triangle edge opposite the 30 degree angle is opposite = tanθ * adjacent.
4. The long edge to the triangle can be calculated by using Pythgoras’ theorem: a² + b² = c²

The code in its etirety becomes too complicated to explain in written English, but it is all based on the simple trigonometry and logic above: https://github.com/gperilli/rhombile/blob/master/src/setLayout.js .

Sketched out on paper it looks like this:

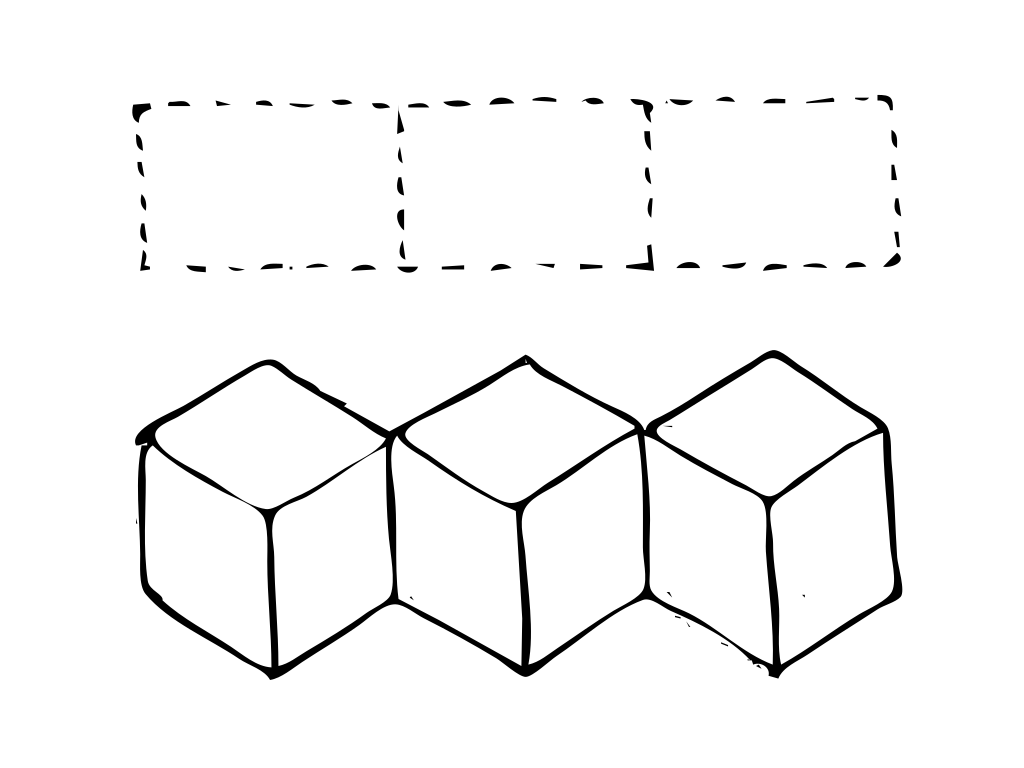1) the rhombile heaxgons on top of their rectangle containers

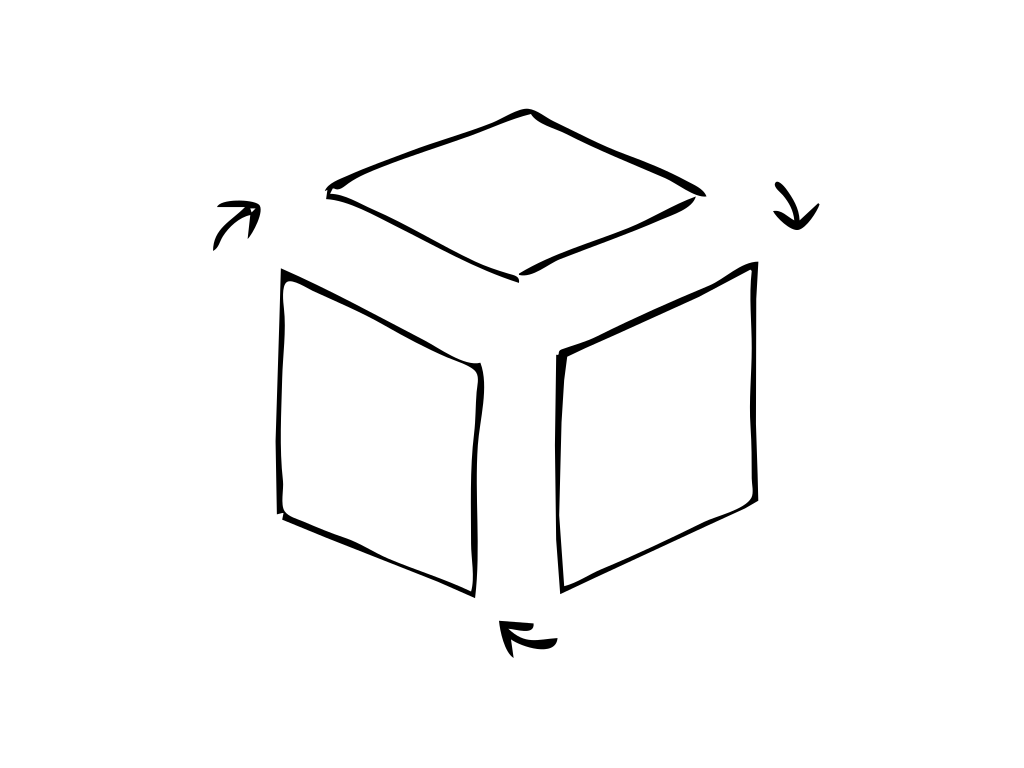2) the rhombile cube formed from three identical rhombi

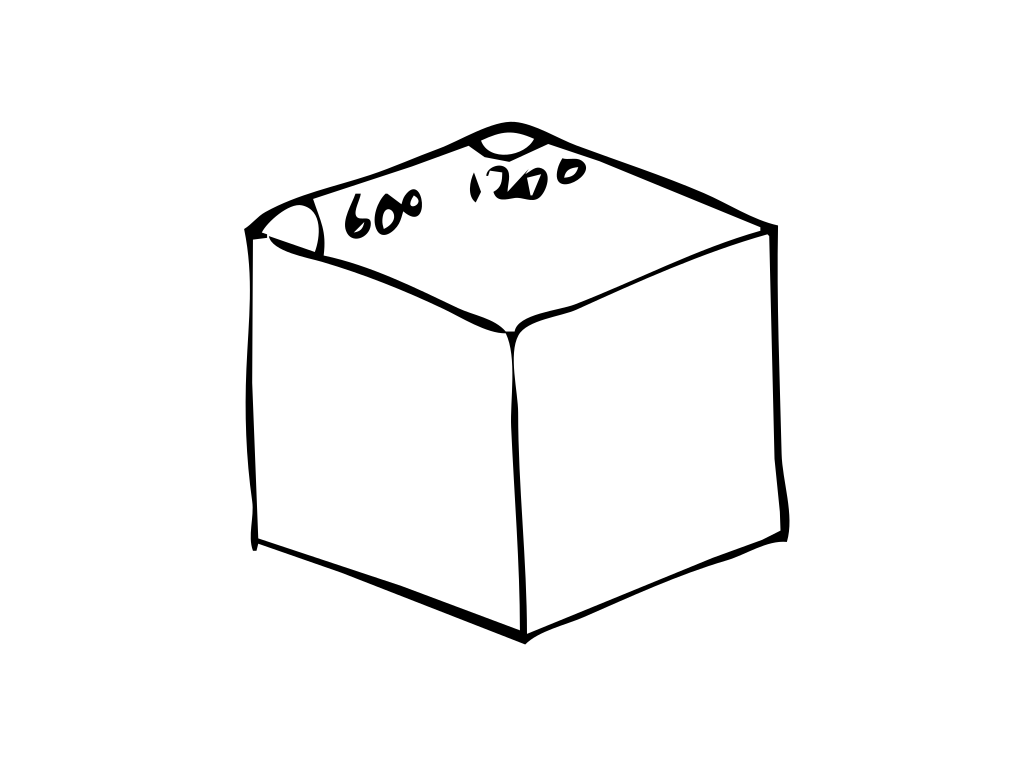3) the rhombi tile angles

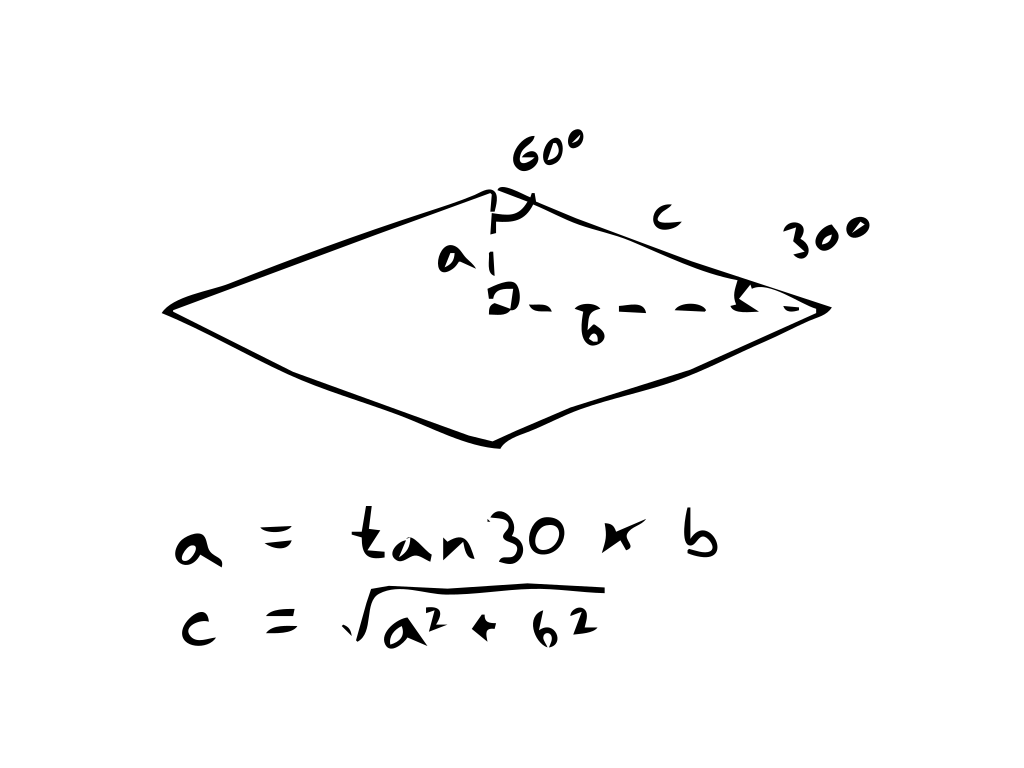4) using trigonometry to calculate the rhombus height (a in the diagram) and Pythagoras' theorem to calculate rhombi side lengths

For more inofrmation on this, take a look at the wikipedia page, and this simple explanation of sin, cos, and tan: https://www.mathsisfun.com/sine-cosine-tangent.html.

Here is a single tile I have put on Codepen:

See the Pen rhombile by Gareth Perilli (@gperilli) on CodePen.

This rhombile cube placed is in a square however. (In my mosaic generator all of the cubes were put into rectangles with the top and botton part of the hexagon / cube overflowing onto the rectangkes above and below.)

Rendering A Mosaic

So far I have developed a number of options to render some rhombile tiling patterns using inline SVG in HTML. Here is the output of some of these:

1) rhombi opacity fade

2) just outlines

3) cube opacity fades

4) random colors assigned to cubes